Clustering Analysis

Clustering reveals the coarse-grained structure of data. However, to understand, evaluate, and leverage data clusterings, we need to quantitatively compare them. Clustering comparison forms the backbone of many tasks, including method evaluations, consensus clustering, and tracking the temporal evolution of clusters.

Take, for example, the evaluation of a clustering or community detection method. To determine if the method is recovering a known feature of the data, it is necessary to compare the method’s result to a planted reference (a.k.a. ground truth) clustering, assuming that the more similar the method’s solution is to the reference clustering, the better the method.

Despite the importance of clustering comparison, no consensus has been reached for a standardized assessment; many, many clustering similarity methods exist, and each similarity measure rewards and penalizes different criteria, sometimes producing contradictory conclusions. The situtation is even worse for generalized definitions of clusterings that include overlaps or hierarchy.

Here I show that existing clustering similarity measures are very poor at measuring differences in heterogeneously sized clusters commonly found in social applications, and no measure was available for overlapping and hierarchically structured clusterings.

To solve these problems, I first modified two popular clustering similarity measures (ARI and NMI) by expanding the definition of random clusters from the permutation model (which fixes the sizes and numbers of clusters) to more realistic random set-theoretic models (which allow for cluster sizes and numbers to vary). These modifications revealed that certain clustering methods would appear to perform well in the context of permutation models, yet, in the context of realistic random-set models, performed worse than randomly generated solutions.

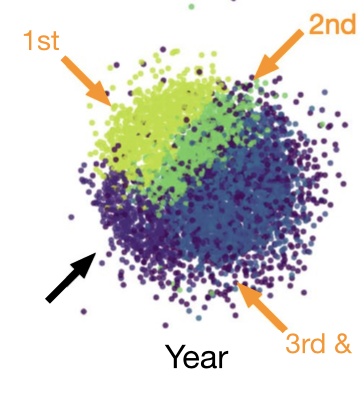
Second, I proposed a new way of thinking about clustering similarity in terms of the connectedness of the data elements (rather than the overlap of clusters). This new element-centric clustering similarity measure naturally accommodates overlapping and hierarchical clusterings. Using the element-wise contributions to this new method, I can trace how community structures change across different regions of the network; for example, in a Facebook social network (Figure above), the dormitory is well aligned to network structure for freshman and sophomores, but fails to reflect friendships amongst juniors and seniors.

Read More: